på 2024/08/27 411

Icke-sinusformade vågformer: fyrkantiga, rektangulära och pulserade vågformer

Inom elektronisk teknik är generering och formning av elektriska vågformer viktiga uppgifter som används inom många områden inklusive kommunikationssystem och digital elektronik.Den här artikeln diskuterar tre typer av vågformer: fyrkantiga vågor, rektangulära vågor och pulserade vågor, var och en med unika egenskaper och användningar.Fyrkantiga vågor symmetri och snabba övergångar mellan tillstånd är det som gör dem så effektiva för att byta applikationer.Rektangulära vågor flexibilitet är användbar i uppgifter som pulsbreddmodulering (PWM) och signalbehandling, där finjustering av vågformen krävs.Pulserade vågor är oregelbundna och icke-upprepade, gjorda för situationer där tidsförändringar används för att skicka information.

Den här artikeln undersöker de fysiska egenskaperna hos dessa vågformer, hur de uppför sig i Fourier -analys och deras praktiska användning.Att förstå dessa detaljer hjälper till att lyfta fram vad som skiljer varje vågform i elektroniska applikationer.Den undersöker också hur varje vågform genereras och de vanliga användningarna för var och en, vilket ger en tydligare bild av hur de bidrar till att förbättra elektroniska mönster.

Katalog

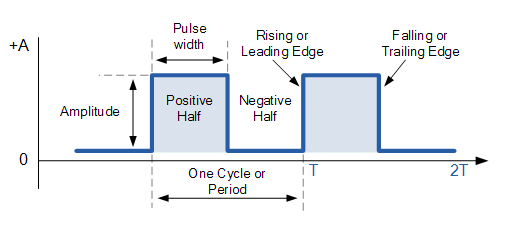
Bild 1: fyrkantig vågform

Egenskaper hos fyrkantiga vågor

Fyrkantiga vågor är vågformer som snabbt växlar mellan två spänningsnivåer som kallas "höga" och "låga."Dessa förändringar sker direkt, vilket skapar en kraftig förskjutning mellan de två staterna.Men i verkliga system bromsar faktorer som kretsegenskaper övergångarna.Den tid det tar för spänningen att stiga eller hösten kallas stigningstid (för att gå upp) och hösttid (för att gå ner).En perfekt fyrkantig våg spenderar lika tid i de höga och låga tillstånden och skapar en balanserad vågform.

Den tid som spenderas i de höga och låga tillstånden kan skilja sig men vågen betraktas fortfarande som en fyrkantig våg.Att ändra denna balans kan vara användbar för olika uppgifter.Men när timingnoggrannhet som i kommunikationssystem är det viktigt att behålla symmetrin.I dessa fall kan extra designjusteringar krävas.

Egenskaper hos rektangulära vågor

Rektangulära vågor liknar fyrkantiga vågor men har ojämna höga och låga faser, vilket ger dem mer flexibilitet.Medan fyrkantiga vågor har lika höga och låga tider, låter rektangulära vågor justera dessa tider separat.Detta gör rektangulära vågor mer användbara för situationer där det strikta mönstret för fyrkantiga vågor inte krävs.

En stor fördel med rektangulära vågor är deras flexibilitet.Genom att justera de höga och låga tiderna kan bredden på varje puls styras som är viktig vid pulsbreddmodulering (PWM).PWM används i saker som motorstyrning, kommunikation och kraftsystem, där tidpunkten måste vara exakt.Rektangulära vågor är också stora vid signalbehandling och tidpunkt.I digital elektronik kan till exempel rektangulära vågor användas som klocksignaler med justerbara tidpunkter för att hjälpa till att samordna olika delar av ett system.Rektangulära vågor är mer flexibla än fyrkantiga vågor eftersom deras pliktcykel kan justeras.

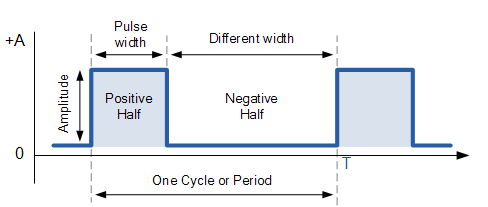
Bild 2: Rektangulär vågform

Egenskaper hos pulserade vågor

Pulserade vågformer skiljer sig från periodiska vågformer eftersom de inte har ett regelbundet, upprepande mönster.Periodiska vågformer upprepas i en jämn cykel men pulserade vågformer inträffar som reaktion på något som att nå en viss spänning.På grund av detta kan pulserade vågformer se annorlunda ut beroende på situationen.

En viktig sak med pulserade vågformer är att de kan bära information genom att ändra form och timing.Periodiska vågformer är mer förutsägbara men pulserade vågformer kan justeras i realtid för att visa olika typer av data.Eftersom pulserade vågformer kan ändras baserat på olika förhållanden är de ett bra verktyg för att hantera komplex information.Deras förmåga att anpassa sig snabbt gör dem viktiga för tekniker som behöver snabba svar och flexibilitet.

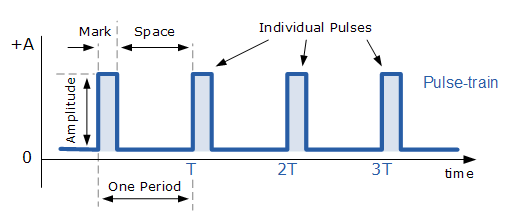
Bild 3: Pulsvågform

Ljud av en fyrkantig, rektangulära och pulserade vågor

Fyrkantiga vågor: Fyrkantiga vågor har ett djärvt, skarpt ljud som sticker ut.De skapar detta starka ljud eftersom de har massor av udda harmonier, vilket ger dem en livlig ton.Vågen växlar snabbt mellan höga och låga nivåer som gör sitt ljud "vilda" och kan klippa igenom andra ljud i en blandning.Fyrkantiga vågor används i elektronisk musik och syntor eftersom de kan göra både djup bas och skarpa, uppmärksamhetsledningar.

Rektangulära vågor: Rektangulära vågor är mer flexibla än fyrkantiga vågor eftersom du kan ändra deras ton genom att justera hur länge de stannar i "höga" position.När tiden är hög är ungefär hälften, låter de som fyrkantiga vågor med en ljus och rik ton.Men om tiden i det höga tillståndet blir kortare blir ljudet tunnare och mer nasal.Denna flexibilitet låter rektangulära vågor skapa ett brett utbud av ljud från starkt och punchy till ljus och ihåligt.

Pulserade vågor: Pulserade vågor har ett snabbt, skarpt ljud, vilket gör dem bra för rytmiska eller korta, slagverk.De är bra på att skapa snabba ljud som klick eller pip och fungerar bra i musik som behöver starka, rytmiska element.Den snabba stigningen och fallet av pulserade vågor ger dem en aggressiv känsla, så de används ofta för synth -stak.

Fourier -analys av fyrkantiga, rektangulära och pulserade vågor

Fyrkantiga vågor

En fyrkantig våg är en vågform som snabbt växlar mellan ett högt och lågt värde och spenderar lika tid på varje nivå.Genom att använda Fourier -serien kan vi uttrycka det som en summa av sinusvågor.För en fyrkantig våg med amplitud A och period t är Fourier -serien:

Här representerar N bara de udda heltalen, och är vågens frekvens.Serien börjar med frekvensen (när ) och innehåller högre udda harmonier.Varje på varandra följande harmoniska minskar i amplituden, efter det omvända av det harmoniska antalet.

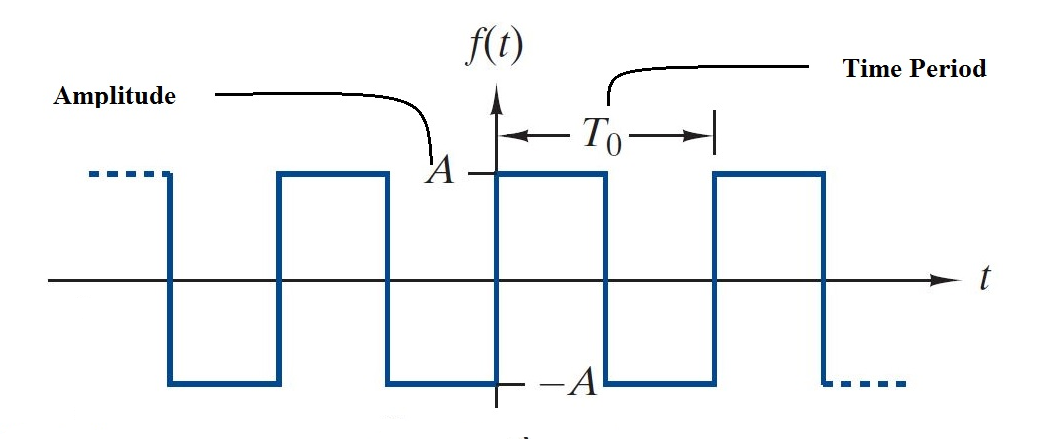
Bild 4: fyrkantiga vågor i Fourier -serien

Rektangulära vågor

Rektangulära vågor liknar fyrkantiga vågor, men tiden i de höga och låga tillstånden är ojämlik.I det här fallet måste Fourier -serien redogöra för "Duty Cycle" D, som är bråkdelen av den period som vågen förblir i det höga tillståndet.Fourier -serien för en rektangulär våg är:

Denna formel justeras för de olika längderna på de höga och låga tillstånden och innehåller driftcykeln D i sinusvågkomponenterna.

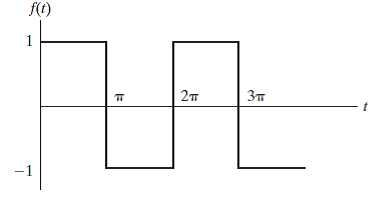
Bild 5: Rektangulära vågor i Fourier -serien

Pulserade vågor

Pulserade vågor eller pulståg består av upprepade pulser separerade med intervaller där signalen är noll.Fourier -analysen av pulståg är mer komplicerad eftersom det beror på formen på pulserna och tidpunkten mellan dem.En vanlig Fourier -serie för ett tåg med rektangulära pulser ser ut:

I detta uttryck är 5 bredden på varje puls, t är perioden mellan pulser, är basfrekvensen för pulståget.De funktion, definierad som , beskriver hur pulsformen påverkar frekvenskomponenterna.

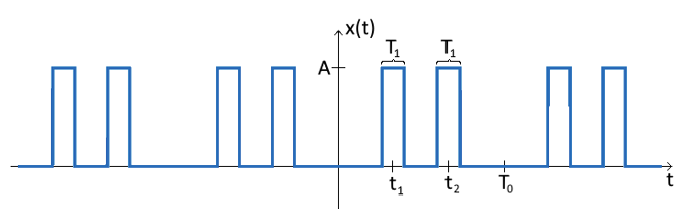
Bild 6: Fourier -analys av pulståg

Elektriska vågformer Exempel

Kvadratvåg

En fyrkantig våg är en av de enklaste typerna av vågformer.Det växlar mellan två nivåer, höga och låga utgifter lika mycket tid i varje stat.Denna lika uppdelning kallas en 50% arbetscykel.

Här är vad det betyder:

• Vågen förblir "på" under en viss tid (hög nivå).

• Den förblir sedan "av" under en lika tidsperiod (låg nivå).

Till exempel, om pulsbredden är 10 millisekunder (MS) för både "på" och "off" -tillstånd, är den totala tiden för en fullständig cykel (en period):

Vågens frekvens berättar hur många cykler som händer per sekund.För att hitta frekvensen använder du formeln:

I det här fallet:

Så vågen upprepar 50 gånger per sekund.

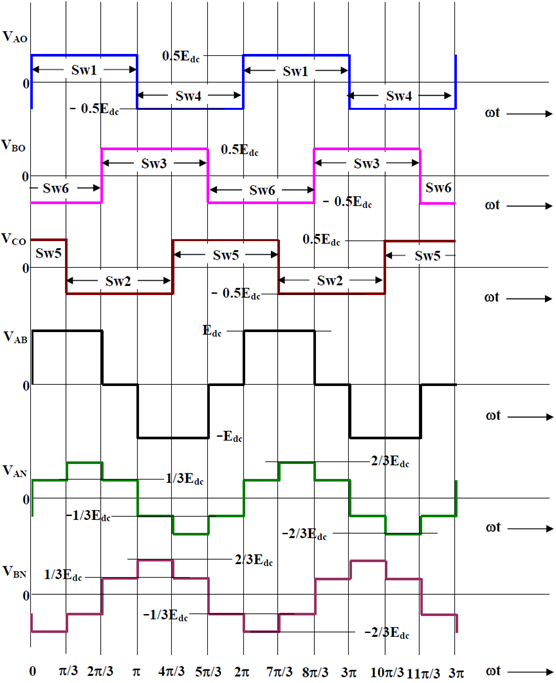
Bild 7: 3-fas spänningskälla inverterare med fyrkantig vågutgång

Rektangulär våg

Låt oss nu utforska rektangulära vågformer, som liknar fyrkantiga vågor men inte har lika med och på tider.Den tid signalen förblir hög kallas den positiva pulsbredden, och förhållandet mellan den tiden och den totala perioden kallas arbetscykeln.

Om den positiva pulsbredden är 10 ms men tullcykeln är 25%, betyder det att vågen är "på" för endast 25% av den totala cykeln.

För att hitta den totala perioden, dela den positiva pulsbredden efter arbetscykeln:

För att hitta frekvensen, använd samma formel som tidigare:

Så den här vågformen skulle upprepa 25 gånger per sekund med "på" tiden som är kortare jämfört med "off" -tiden.

Jämförelse av fyrkantiga vågor, rektangulära vågor och pulserade vågformer

Karakteristisk	Fyrkantiga vågor	Rektangulära vågor	Pulserade vågformer
Form	Symmetriska, lika höga och låga tider	Asymmetrisk, förändrad driftscykel	Skarpa, plötsliga pulser med olika bredd
Amplitud	Konstant	Konstant	Konstant
Frekvens	Fixat baserat på ansökan	Justerbar	Lägre än basfrekvens
Puls Bredd	Halva perioden (vid 50% arbetscykel)	Beroende av arbetscykel	Mycket kort till måttlig, definierar puls
Upprepning Hastighet	Definieras av frekvens	Definieras av frekvens	Låg till mycket hög
Tull Cykel	50% (fast)	Varje procentandel, inte 50%	Varierar mycket, mindre än 50%
Harmonisk Innehåll	Rik på udda harmonik	Rik på harmonik	Beroende av pulsform och bredd
Generation Metod	Oscillatorer, flip-flops	Justerbara oscillatorer, signalgeneratorer	Pulsgeneratorer, specialiserade kretsar
Ansökningar	Tidskretsar, digitala klockor	Växla strömförsörjning, modulatorer	Radar, kommunikation, medicinsk avbildning

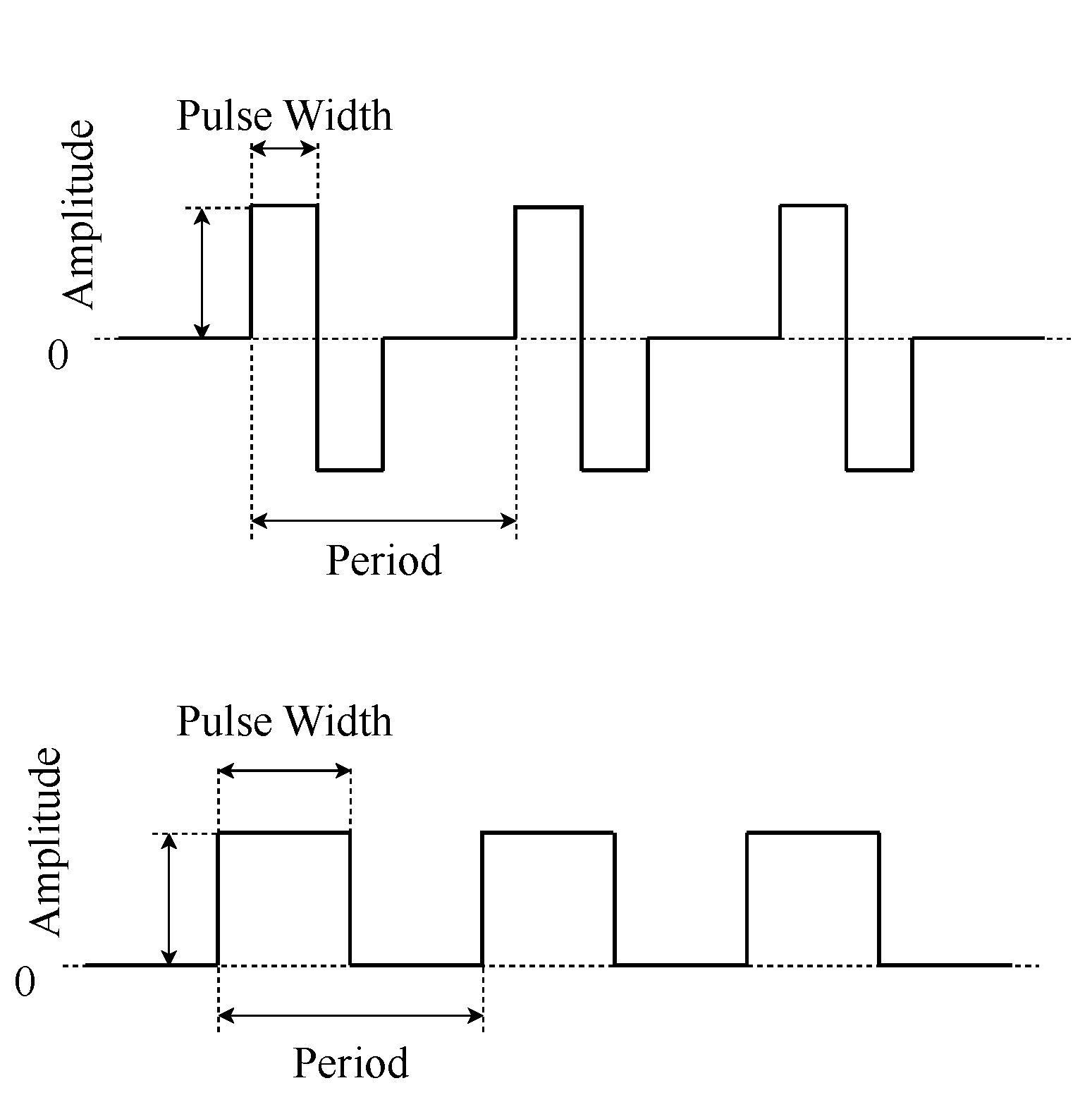
Bild 8: fyrkantig och rektangulär våg

Slutsats

Den här artikeln förklarar vikten av olika typer av vågformer i utformningen av elektroniska system.Varje vågform har sina egna egenskaper och fördelar som är användbara i specifika situationer.Fyrkantiga vågor är användbara för digitala system.De säkerställer smidiga och exakta övergångar mellan binära tillstånd som är bra för databehandling och kommunikation.Rektangulära vågor utvidgar detta koncept genom att tillhandahålla justerbara pliktcykler, vilket möjliggör mer exakt kontroll i applikationer där signaltid måste anpassas.Pulserade vågor är ovärderliga i situationer som kräver hög flexibilitet och lyhördhet, såsom radar eller medicinsk avbildning.De förmedlar information genom förändringar i pulsform och timing, vilket gör dem idealiska för att överföra data.Fourier -analys av dessa vågformer erbjuder en tydlig, matematisk förståelse av deras beteende.Den här artikeln ger en tydlig översikt över både teorin och praktiska användningar av dessa vågformer, vilket gör den till en värdefull guide för alla som arbetar inom elektronisk design.

Vanliga frågor [FAQ]

1. Vilka är fördelarna med fyrkantiga vågor?

Fyrkantiga vågor värderas eftersom de är enkla och användbara i många elektronik- och signalbehandlingsuppgifter.En stor fördel är deras skarpa växel mellan höga och låga nivåer, vilket gör dem perfekta för timing och digitala klocksignaler i datorer och andra digitala enheter.Dessa snabba förändringar hjälper till att undvika förvirring vid läsningssignaler.Dessutom har fyrkantiga vågor bara udda harmonier som gör dem lättare att arbeta med i applikationer som involverar harmonier, som synthesizers och ljudteknologi, där tydliga ljud är viktiga.

2. Hur tillverkas fyrkantiga vågor?

Fyrkantiga vågor genereras med hjälp av elektroniska oscillatorer, såsom Schmitt-triggers eller flip-flop-kretsar, som växlar mellan två spänningsnivåer.Dessa oscillatorer byter utgångar när deras ingång korsar vissa tröskelvärden, vilket skapar de skarpa övergångarna som är karakteristiska för fyrkantiga vågor.Funktionsgeneratorer som används i laboratorier kan också programmeras för att producera fyrkantiga vågor med önskad frekvens och amplitud genom att snabbt växla mellan höga och lågspänningsstillstånd.

3. Vad är den rektangulära pulsperioden?

Perioden för en rektangulär puls hänvisar till varaktigheten för en fullständig cykel för pulsen, som omfattar ett högt tillstånd och ett lågt tillstånd.Detta kvantifieras som den tid det tar för pulsen att återgå till sitt ursprungliga tillstånd.Perioden t för pulsen är summan av varaktigheten för det höga tillståndet (TTHIGH) och det låga tillståndet (tlow), uttryckt som t = lår+tlow.I praktiska termer bestämmer denna period frekvensen för pulsvågformen med frekvensen som periodens ömsesidiga (f = 1/t).

4. Vilka är komponenterna i pulsvågformen?

En pulsvågform består av flera komponenter:

Amplitud: det maximala värdet för pulsen över eller under dess baslinje.

Varaktighet: Längden för pulsen är vid sin maximala amplitud.

Stigningstid: Tiden tar för pulsen att övergå från dess låga värde (ofta mark eller nollspänning) till dess höga värde.

Hösttid: Tiden tar för pulsen att övergå från sitt höga värde till sitt låga värde.

Tullcykel: representerar andelen av en period där signalen är aktiv eller hög.Det uttrycks ofta i procent.

5. Hur mäts pulsvågformen?

Här är processen:

Anslut oscilloskopproberna till signalkällan eller enheten som matar ut pulsvågformen.

Justera oscilloskopinställningarna som tid/uppdelning och volt/division för att på lämpligt sätt skala vågformen på skärmen.

Trigger oscilloskopet för att stabilisera vågformsdisplayen och se till att pulsen är rent och stadigt visualiserad.

Använd oscilloskopets mätverktyg för att bestämma pulsens amplitud, period, arbetscykel, stigningstid och falltid direkt från den visade vågformen.