Hur fungerar grindar med flera ingångar?
Inom det expanderande området för digital elektronik bildar logikgrindar ryggraden i beräkningsprocesser, vilket möjliggör genomförandet av logiska operationer som är kärnan i modern teknik.Dessa grindar, som varierar från enkla inte grindar till komplexa exklusiva eller (XOR) och exklusiva-Nor (XNOR) grindar, fungerar som de farliga byggstenarna för intrikata digitala kretsar.Genom att utnyttja olika typer av teknik, såsom transistor-transistor logik (TTL) och kompletterande metalloxid-sememeduktor (CMO), kan dessa grindar skräddarsys för att uppfylla specifika kraft, hastighet och effektivitetskrav.Den här artikeln undersöker djupt i den operativa mekaniken, applikationerna och typer av olika digitala logikgrindar, vilket ger en grundläggande förståelse för deras roll i elektronik.Den undersöker de viktigaste skillnaderna mellan TTL- och CMOS -teknologier, mångsidigheten hos grindar som NAND och inte heller för att konstruera komplexa logiska funktioner och de nyanserade operationerna av XOR- och XNOR -grindar i avancerade beräkningskretsar.Denna fullständiga utforskning understryker vikten av logiska grindar vid utformningen av funktionaliteten och effektiviteten hos moderna digitala system.Katalog
Digitala logikgrindar
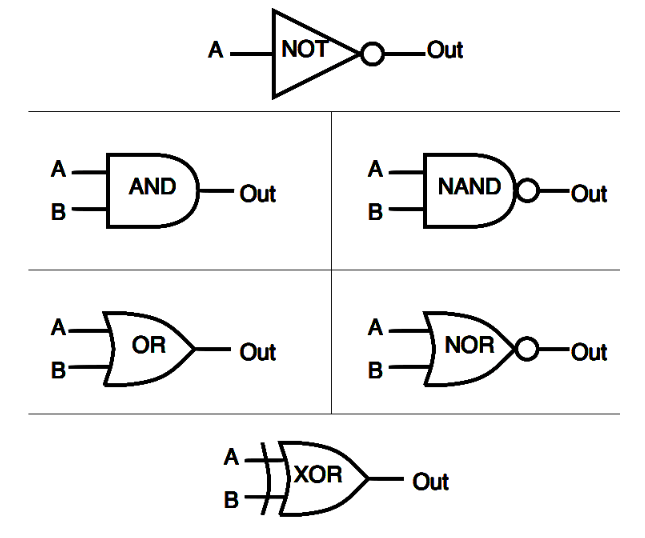
Bild 1: Digitala logikgrindar
Digitala logikgrindar är grundläggande komponenter inom elektronik, som används för att utföra logiska operationer baserade på digitala signalstillstånd.Varje grind har vanligtvis flera ingångar (märkt A, B, C, D) och en utgång (Q).Genom att ansluta dessa grindar kan vi skapa kretsar som sträcker sig från enkla kombinationssystem till komplexa sekventiella inställningar, vilket möjliggör avancerade logiska funktioner med hjälp av basiska grindar.
De vanligaste typerna av grindar är transistortransistor logik (TTL) och kompletterande metalloxid-kisel (CMO).TTL -grindar använder bipolära övergångstransistorer (BJT), inklusive både NPN- och PNP -typer, som möjliggör snabb omkoppling och hög drivfunktioner.Däremot använder CMOS -teknik par MOSFET: er eller JFET: er i kompletterande arrangemang, vilket avsevärt minskar kraftförbrukningen på grund av minimal aktuell dragning när den är i statisk tillstånd.Denna skillnad belyser de distinkta metoderna för digital signalbehandling i olika grindfamiljer.
Valet mellan TTL och CMO kan påverka kretskonstruktionen på grund av deras olika elektriska egenskaper.TTL -grindar växlar snabbare, vilket gör dem idealiska för farliga applikationer, men de konsumerar mer kraft och genererar mer värme.För att hantera detta måste operatörerna ofta använda kylsystem eller kylflänsar för att upprätthålla prestanda.
Å andra sidan föredras CMOS Gates i batteridrivna eller energikänsliga applikationer eftersom de konsumerar mindre kraft.De drar minimal kraft i ett statiskt tillstånd och sprider endast kraft under omkopplingshändelser.Detta kräver exakt tidpunkt och kontroll för att optimera effekteffektiviteten och minimera värmen under snabb växling.
Vad är inte grind?
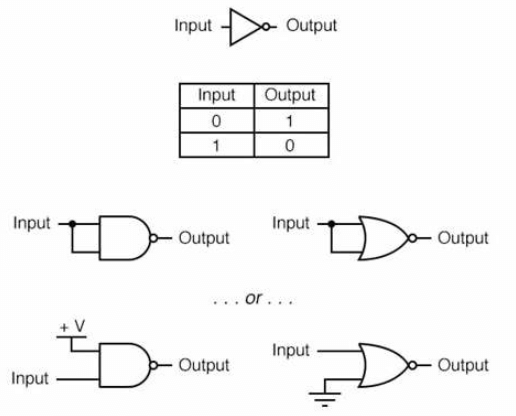
Bild 2: Kretsdiagram för inte grind
NOT -grinden, även kallad en inverterare, är en kärnig digital logikport som tar en inmatning och matar ut dess motsats.Om ingången är hög (sant) kommer utgången att vara låg (falsk), och om ingången är låg kommer utgången att vara hög.Denna enkelhet gör inte grinden till en idealisk utgångspunkt för att lära sig om digital logik.
Operatörer kan se olika symboler och representationer av inte grindar beroende på regionala och internationella standarder.Denna variation belyser portens utbredda användning och huvudsaklig betydelse i digital design.Trots sin enkelhet behövs inte grinden i mer komplexa operationer, till exempel att skapa växelförhållanden i flip-flops eller kontrollera timingelement i synkrona kretsar.
Vanliga tillämpningar av inte grind
Dess mest enkla tillämpning är logiksignalinversionen, grundläggande i digitala kretsar där en viss logikoperation kräver motsatt logiktillstånd.Inte grindar genererar kompletterande signaler i system, särskilt behövs i minnes- och bearbetningskretsar.Genom att kombinera en inte grind med komponenter som kondensatorer och motstånd kan enkla oscillatorer skapas, vilket genererar en kontinuerlig kvadratvågsignal som används vid timing och kontrollapplikationer.I kontrolllogikkretsar säkerställer inte Gates att specifika förhållanden uppfylls innan en åtgärd inleds, såsom inaktivering av en del av en krets om inte alla säkerhetsförhållanden är uppfyllda.De är också instrumentella i komplexa digitala kretsar tillsammans med andra logiska grindar, såsom och eller grindar, för att bygga sofistikerade funktioner för enheter som multiplexerare, avkodare och aritmetiska logikenheter.Inte grindar spelar en roll i att avlägsna kretsar som stabiliserar signaler från mekaniska switchar och knappar för att förhindra falsk utlösning.De används också i signalkonditionering för att upprätthålla signalintegritet, och skyddssignaler läses korrekt av digitala ingångar.
Vad är och grind?
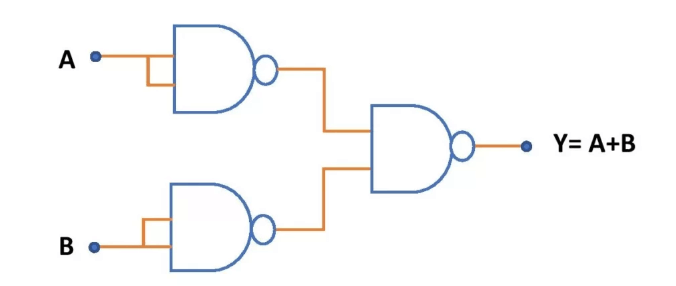
Bild 3: Nand Gate Circuit Diagram
Och grinden är en kärnkomponent inom digital elektronik som utför en logisk konjunktion som liknar aritmetisk multiplikation.Den producerar en hög produktion endast när alla dess ingångar är höga, vanligtvis representerade av en prick (.) I scheman.Denna grind behövs i applikationer som sträcker sig från grundläggande aritmetiska kretsar som tillägg till komplexa system som trafikstyrning och säkerhetsapplikationer.
Det krävs för exakta kontrolloperationer.I aritmetiska kretsar som adderare och multiplikatorer synkroniserar och är grind flera signaler för att säkerställa exakta beräkningar.I trafikhanteringssystem och grindar koordinerar signaler för att säkerställa att trafikflödesförändringar endast inträffar under säkra förhållanden.
Två typer av och grindar
• 3 -ingång och grind - Det är en digital logikport som matar ut en hög signal endast om alla tre ingångarna är höga, fungerar baserat på den logiska "och" Operation Principal in Digital Electronics.Symbolen innehåller tre rader som kommer in i en enda grind, som symboliserar att alla ingångar måste vara sanna för att utgången ska vara sanna.Denna typ av grind används i olika applikationer, till exempel beslutskretsar där den styr mekanismer som endast aktiveras när tre separata förhållanden upptäcks av sensorer.Det behövs i säkerhetssystem, för att säkerställa att maskiner endast fungerar under säkra förhållanden, till exempel en press som endast fungerar när säkerhetsvakterna är på plats, operatören är på ett säkert avstånd och rätt driftsläge väljs.3-ingång och grindar är idealiska för elektroniska kombinationslås, vilket kräver tre korrekta ingångar för att låsa upp en mekanism.I komplexa kontrollsystem som finns i robotik eller automatiserade produktionslinjer säkerställer dessa grindar åtgärder endast när flera förutsättningar uppfylls, inklusive positionsdata och systemberedskap.
• 2-ingångstransistor och grind-En grundläggande 2-ingångstransistor och grind kan konstrueras med hjälp av motståndstransistor logik (RTL), vilket kräver att båda transistorerna ska vara aktiva (på) för att utgången ska vara hög.Denna installation är särskilt användbar för att förstå elektroniskt signalflöde och de nödvändiga förhållandena för att uppnå önskad utgång.Och grindar behövs i verkliga system, till exempel trafikljuskontroll där de säkerställer att lamporna endast förändras när flera säkerhetsförhållanden uppfylls, vilket förhindrar olyckor.I säkerhetssystem och grindar samordnar svar på flera sensoringångar, vilket garanterar att larm endast utlöser under specifika förhållanden.Och grinden krävs i digitala system, hantering av synkroniserade ingångar för att producera exakta utgångar.Dess tillämpningar sträcker sig från enkla aritmetiska operationer till farliga roller i trafik- och säkerhetssystem, där exakta villkorade svar är grundläggande.
Vad är Nand Gate?
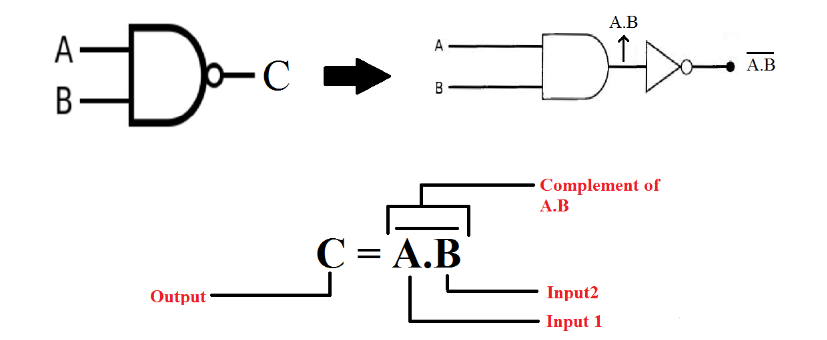
Bild 4: NAND Logic Gate Circuit Diagram
Nand -porten är den logiska inversa av och grinden.Den matar ut en låg signal endast när alla ingångar är höga;Annars matar det ut högt.Utformningen och driften av NAND-grinden är kärna, särskilt när man använder CMOS-teknik där konfigurationen av n-typ och p-typ transistorer möjliggör effektiv växling och minimal effektläckage, grundläggande för batteridrivna enheter.Portens förmåga att upprätthålla en hög produktion under de flesta förhållanden hjälper till att spara kraft, vilket gör den ovärderlig i energikänsliga applikationer.
NAND -grindar är extremt mångsidiga, används i allt från grundläggande säkerhetssystem, där de endast kan utlösa larm under specifika förhållanden och därmed höja tillförlitligheten och minska falska larm till komplex beräkningslogik.De är grundläggande när de konstruerar andra grundläggande grindar som och, och inte genom olika kombinationer, understryker deras farliga roll i digital kretsdesign.Utöver enkla grindar är NAND -grindarna instrumentella i att skapa mer komplexa logiska kretsar och sekventiella enheter, och spelar en nyckelroll i minneslagring och återhämtning i beräkningsenheter, som visar deras breda användbarhet i modern elektronik.
Olika typer av NAND -grind
• Grundläggande NAND -grind - En grundläggande NAND -grind är den vanligaste typen av digital logikport, och den utför det logiska komplementet för och grindens funktion.Den har två eller flera ingångar och en utgång.I huvudsak kommer en NAND -grind att mata ut en hög signal (1) såvida inte alla dess ingångar är höga (1), i vilket fall den matar ut en låg signal (0).Denna grind representeras symboliskt av en och grind med en inversionscirkel vid utgången, vilket anger den inte operation som tillämpas på och grindens resultat.
• NAND -grind med flera ingångar - Denna grind utvidgar det grundläggande NAND -grindkonceptet till tre eller flera ingångar.Liksom sin enklare motsvarighet är utgången från en NAND-grind med flera ingångar bara låg om alla dess ingångar är höga.Ökningen i antalet ingångar möjliggör mer komplexa logiska funktioner och integrationer i kretsar, vilket minskar behovet av flera två-ingångsgrindar i serie eller parallella konfigurationer.
• Schmitt Trigger NAND GATE - En grind innehåller en Schmitt -triggermekanism, som lägger till hysteres till övergången till ingångsutgången.Detta innebär att spänningströsklarna för växling från hög till låg och låg till hög är olika.Sådana grindar är särskilt användbara i miljöer med bullriga signaler där ingången kan variera, eftersom hysteresen hjälper till att stabilisera utgången genom att minska falska övergångar.
• CMOS NAND GATE-Dessa grindar är gjorda av par av P-typ och N-typ MOSFETS arrangerade för att utföra NAND-funktionen.CMOS-tekniken är uppskattad för sin låga kraftförbrukning och immunitet med hög brus, vilket gör den idealisk för batteridrivna enheter och storskalig integration i mikroprocessorer och andra digitala IC: er.
• TL NAND GATE - TTL (transistor -transistor logik) NAND -grindar använder bipolära korsningstransistorer (BJTS) och motstånd.Även om de i allmänhet konsumerar mer kraft och är mindre brusimmun jämfört med CMOS-grindar, är TTL NAND-grindarna snabbare, vilket behövs i applikationer där hastighet är en farlig parameter.
• Open Collector NAND GATE - Open Collector Nand Gates har ett unikt utgångssteg där utgångstransistorn endast drar linjen låg (aktiv låg).Ett externt motstånd måste dra linjen högt när utgångstransistorn är av.Denna konfiguration används i situationer där flera enheter behöver dela en enda utgångslinje, ofta sett i bussar eller andra inställningar för kommunikation av flera enheter.
Logik eller grind
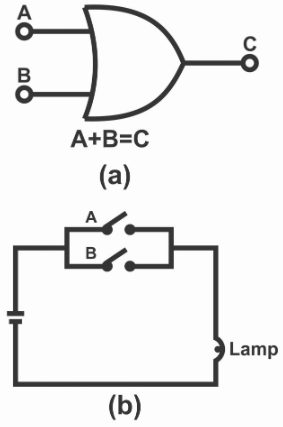
Bild 5: Logik eller grinddiagram
OR -grinden är en grundläggande digital logikkomponent som matar ut en hög signal om någon av dess ingångar är höga.Denna funktionalitet behövs för kretsar som måste reagera positivt på alla höga signaler, vilket gör den grundläggande i system som kräver inkludering vid signalbehandling.
Denna typ av grind är grundläggande i scenarier som kräver beslut baserat på flera inmatningsvillkor.I automatiserade system kan till exempel en eller grind kontrollera ställdonssvar på olika sensoringångar, vilket bekräftar att åtgärder vidtas om något villkor uppfylls.Operatörer måste förstå nyanserna av OR -portens beteende, särskilt dess förmåga att snabbt bearbeta och svara på förändrade ingångar, en funktion som behövs i dynamiska miljöer.Denna känslighet krävs särskilt i säkerhetssystem, där snabb upptäckt av alla farliga tillstånd måste utlösa ett omedelbart förebyggande svar.
Användning av logik eller grind
Logiken eller grinden används i stor utsträckning i larmsystem och kan initiera en varning om någon av flera sensorer upptäcker ett brott.Det är också grundläggande i styrsystem, där det kan säkerställa att en maskin fungerar om något av de nödvändiga förhållandena uppfylls, till exempel säkerhetskontroller eller beredskapssignaler.Eller grindar används i komplex beräkningslogik, som hjälper till att utföra algoritmer som kräver att minst en av flera ingångar är sanna att fortsätta.Deras förmåga att hantera flera förhållanden samtidigt gör dem kärna i både enkla och komplexa digitala system, strömlinjeformning av operationer och höjningssystemets lyhördhet.
Vad är inte GATE?
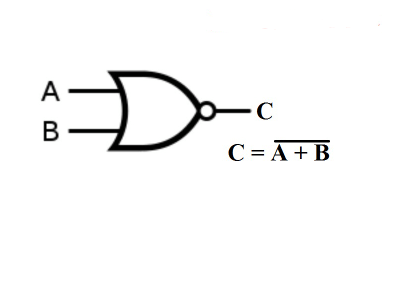
Bild 6: inte heller grind
NOR -grinden är en nyckelkomponent inom digital elektronik och matar ut en hög signal endast när alla dess ingångar är låga.Detta gör det till det logiska inversa av en OR -grind och är grundläggande i digital kretsdesign för universellt negerande ingångar.
Det är särskilt värdefullt på grund av dess exklusiva höga utgång under låga ingångsförhållanden, vilket möjliggör snäv kontroll i digitala system.Till exempel, i ett åtkomstkontrollsystem, säkerställer en NOR -grind att inträde endast är tillåtet när alla specifika säkerhets- och säkerhetsvillkor är ouppfyllda, vilket effektivt förhindrar obehörig åtkomst.Operatörer av sådana system måste skickligt hantera NOR -grindens svarsdynamik, särskilt i komplexa kretsar där flera eller grindar interagerar.Denna hantering kräver ofta noggrann tidpunkt och synkronisering för att uppnå de önskade resultaten, som behövs för att skapa misslyckade mekanismer och villkorade svarssystem.
Dess förmåga att tillhandahålla en hög produktion möjliggör konstruktion av komplexa logikfunktioner med färre komponenter genom att kombinera eller grindar, och därmed minska den totala komplexiteten och kostnaden för kretsen.Inte heller grindar är huvudsakliga för att bygga andra typer av logikgrindar och digitala kretsar, såsom inverterare eller grindar, och ännu mer komplexa konfigurationer, vilket höjer designflexibiliteten.Deras användning av lagringskretsar i minnet, som spärrar, understryker ytterligare deras mångsidighet och effektivitet.
Exklusiv eller grind
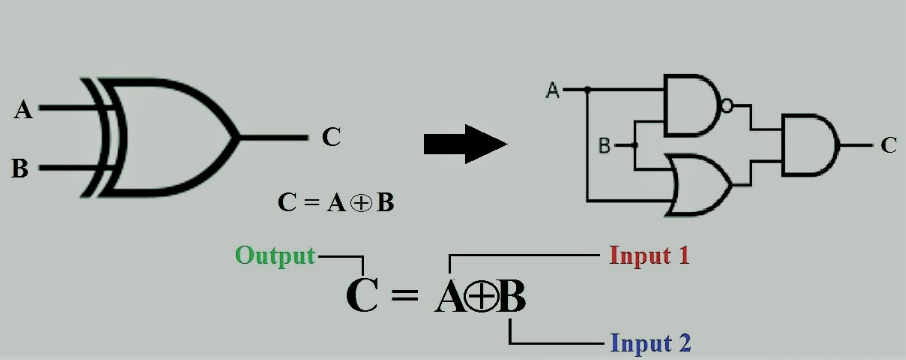
Bild 7: Exklusiv eller grind
Den exklusiva eller (ex-eller) -grinden krävs i beräkningskretsar, utför aritmetiska funktioner och skyddar dataintegritet genom feldetektering.Dess förmåga att skilja mellan olika inmatningstillstånd gör det krävs för exakta logiska operationer i digitala system.
Ex-or Gate är kärnan för uppgifter som binärt tillägg och genomförande av paritetskontroller.I samband med binärt tillägg har ex-eller-grinden i uppdrag att beräkna summan av två bitar, medan en separat mekanism hanterar överföringen.Denna funktionalitet krävs för att stödja mer komplexa aritmetiska operationer inom beräkningsarkitekturer.Tekniker som arbetar med ex-eller-grindar måste noggrant förstå sina unika input-svaregenskaper-grinden producerar en hög produktion endast när ingångarna skiljer sig åt.Korrekt inställning och felsökning av ex-eller-grindar innebär att garantera exakt signaltid och justering, vilket särskilt behövs i sekventiella logiska kretsar där operationens ordning kan påverka resultatet.
Olika typer av exklusiva eller grind
• Grundläggande två-ingång XOR-grind-Basic Two-Input XOR GATE representeras av en standardlogiksymbol med en krökt linje på ingångssidan.Det matar ut när ingångarna skiljer sig från varandra, till exempel i fallet 01 eller 10. Det booleska uttrycket för denna XOR -operation representeras som OR, som inkapslar grindens exklusiva natur, där endast olika ingångskombinationer resulterar i enTrue Output.
• XOR-grind med flera ingångar-Logiksymbolen för en XOR-grind med flera ingångar är en förlängning av den grundläggande XOR-grinden som rymmer fler ingångslinjer.Sanningstabellen är utformad för att matas ut för ett udda antal riktiga ingångar, vilket återspeglar dess paritetslogikfunktionalitet.Vanligtvis realiseras XOR-grindar med flera ingångar genom att kaskadera två-ingång XOR-grindar för att hantera flera ingångar effektivt.
• CMOS XOR GATE-CMOS XOR-grindar använder kompletterande metalloxid-Semiconductor-teknik, som inkluderar både NMO: s och PMOS-transistorer.Denna teknik firas för sin låga kraftförbrukning och hög inmatningsimpedans, vilket gör den särskilt lämplig för batteridrivna enheter.Konfigurationen av CMOS XOR -grindar involverar vanligtvis ett mer komplicerat arrangemang av transistorer än de som finns i TTL -kretsar.
• TTL XOR GATE - TTL XOR -grindar är konstruerade med hjälp av transistor -transistorlogik, som förlitar sig starkt på bipolära korsningstransistorer.Dessa grindar är kända för sin snabba drift och brusolerans, egenskaper som gör dem lämpliga för industriella miljöer.Den typiska konfigurationen innehåller flera transistorer och kan också innehålla dioder för att effektivt inse XOR -funktionen.
• Optical Xor Gate - Optical Xor Gates arbetar med ljussignaler istället för elektriska.De är baserade på principer som interferometri eller olinjära optiska effekter.Dessa grindar är exceptionellt användbara i höghastighetskommunikationssystem och optisk datoranvändning, där traditionella elektroniska grindar kan komma till kort när det gäller hastighet och effektivitet.
• Quantum Xor Gate - När det gäller kvantdatorn implementeras XOR -grindar med hjälp av kvantbitar eller qubits.Dessa grindar behövs för komplexa operationer såsom kvantteleportering och vissa kvantalgoritmer.Kvant XOR-grindar realiseras vanligtvis genom kontrollerade-inte-operationer och andra huvudkvantgrindar, vilket underlättar specifika interaktioner i kvantkretsar.
• Programmerbar XOR -grind - Programmerbara XOR -grindar kan konfigureras inom programmerbara logikenheter, såsom FPGA: er (fältprogrammerbara grindarrayer) eller CPLD (komplexa programmerbara logikenheter).Denna flexibilitet gör att grindarna kan justeras dynamiskt efter de specifika behoven hos olika applikationer, vilket gör dem till grundläggande komponenter inom adaptiv teknik.
Exklusiv-nor
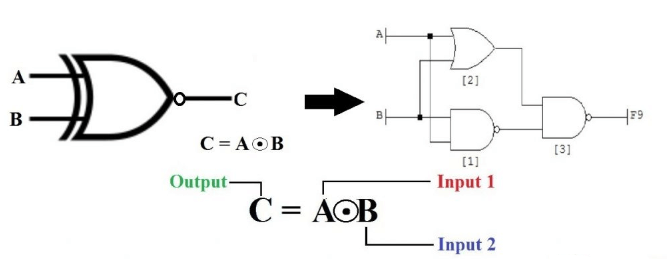
Bild 8: Exklusiv-nor-grind
Den exklusiva-NOR (ex-NOR) grinden fungerar som komplementet till XOR-porten och spelar en nödvändig roll i digitala system som utvärderar inmatningens enhetlighet.Det behövs för applikationer som kräver konsekventa kontroller eller paritetsutvärderingar i digitala sändningar.
Denna grind används i stor utsträckning i digitala kretsar för att verifiera enhetligheten eller jämlikheten hos insignaler, vilket gör det till ett nödvändigt verktyg för att garantera dataintegritet.Denna grind används vanligtvis i felkontrollprocesser för att jämföra bitar från två olika källor, vilket bekräftar deras match för att garantera felfri dataöverföring.För effektiv användning måste operatörer och tekniker vara välbevandrade med ex-NOR-portens strikta utgångsförhållanden-det ger en hög utgång endast när alla ingångar är exakt lika.Detta krav på exakt inputjustering och synkronisering ställer betydande krav på konfiguration och underhåll av digitala system, särskilt i applikationer som dataverifieringssystem och digitala paritetskontroller som beror starkt på strikt datakongruent.
Olika typer av exklusiva-nor-grind
• Standard CMOS XNOR GATE - Detta är den vanligaste typen som används i digitala kretsar.Det består vanligtvis av ett arrangemang av CMO: er (kompletterande metalloxid-sememiconductor) transistorer som uppnår låg effektförbrukning och högbrusimmunitet.Denna grind är idealisk för batteridrivna enheter på grund av dess effekteffektivitet.
• TTL XNOR GATE - TTL XNOR -grindar är gjorda med bipolära transistorer och är kända för sina snabba växlingstider, vilket gör dem lämpliga för höghastighetsoperationer.De tenderar emellertid att konsumera mer kraft jämfört med CMOS -grindar.
• Pass-Transistor Xnor Gate-Den här typen använder pass-transistorlogik, som kan vara mer områdeseffektivt än standard CMOS-logik.Det resulterar ofta i snabbare drift och minskat transistorantal, vilket är fördelaktigt i högpresterande och kompakta digitala kretsar.
• QUANTUM -DOT Cellular Automata (QCA) XNOR GATE - En nyare teknik, QCA använder positionen för elektroner snarare än nuvarande flöde för logikoperationer, vilket erbjuder potentialen för extremt låg effektförbrukning och höga bearbetningshastigheter.Det är fortfarande till stor del i forsknings- och utvecklingsfasen.
• Optical Xnor Gate - Denna typ använder optiska signaler istället för elektriska signaler, vilket gör det användbart i optiska dator- och kommunikationssystem där hög bandbredd och immunitet mot elektromagnetisk störning krävs.
Slutsats
Under denna utforskning av digitala logikgrindar har vi sett hur dessa grundläggande komponenter komponerar symfonin i digital bearbetning.Från enkelhet och grundläggande roll som inte grindar i signalinversion till de nyanserade tillämpningarna av XOR- och XNOR -grindar i feldetektering och korrigering ger varje grindtyp unika egenskaper och fördelar till digital kretsdesign.Kontrasten mellan TTL- och CMOS -teknologier berikar ytterligare landskapet och erbjuder designers val som påverkar systemets prestanda baserat på kraftförbrukning, hastighet och brusimmunitet.De praktiska tillämpningarna framhävde - från grundläggande aritmetiska operationer till sofistikerade säkerhets- och dataintegritetssystem - illustrerar den farliga rollen som dessa grindar spelar över olika tekniska domäner.När tekniken utvecklas kommer den kontinuerliga förbättringen och anpassningen av dessa grindar att vara kärnan i att möta de ökande kraven på snabbare, mer effektiva och mer pålitliga digitala system.Denna resa genom komplikationerna med digitala logiska grindar förbättrar inte bara vår förståelse för elektroniska principer utan belyser också den obevekliga innovationen som driver elektronikindustrin framåt.
Vanliga frågor [FAQ]
1. Vilka enheter använder logikgrindar?
Logikgrindar är grundläggande komponenter i digitala kretsar och används i stor utsträckning i enheter som datorer, smartphones och andra elektroniska apparater.De är också integrerade i drift av automatiserade system som trafikljus och modern industriutrustning.
2. Hur hittar jag utgången från logikgrindarna?
Utgången från en logisk grind bestäms genom att tillämpa ingångsvärdena på grindens specifika logikfunktion (såsom och, eller inte, NAND eller, XOR, XNOR).Till exempel kommer en och grind att mata ut en hög signal (1) endast om alla dess ingångar är höga.Du kan använda sanningstabeller för att enkelt bestämma utgången för alla möjliga ingångskombinationer.
3. Vilka är fördelarna med logiska grindar?
Logikgrindar är enkla, pålitliga och kan användas för att skapa komplexa kretsar genom kombination.De möjliggör konstruktion av digitala system som är skalbara, lätt modifierbara och kan bearbeta information effektivt.Deras förutsägbarhet och binär natur gör dem idealiska för applikationer som kräver exakt kontroll och beslutsfattande.
4. Är logikportens hårdvara eller programvara?
Logikgrindar är främst hårdvarukomponenter tillverkade av halvledarmaterial som kisel.De finns fysiskt i integrerade kretsar eller mikrochips.Emellertid kan begreppet logiska grindar också simuleras i programvara för utbildningsändamål eller digital kretsdesign.
5. Vilka är försiktighetsåtgärderna för logiska grindar?
När du använder logikgrindar är det fördelaktigt att överväga faktorer som spänningsnivåer, kompatibilitet med andra komponenter och att undvika att ladda för många enheter på en enda utgång, vilket kan leda till signalintegritetsproblem.Se till att korrekt hantering för att undvika statisk skada och följa tillverkarens specifikationer för optimal prestanda.
Om oss
ALLELCO LIMITED
Läs mer
Snabb förfrågan
Skicka en förfrågan, vi svarar omedelbart.
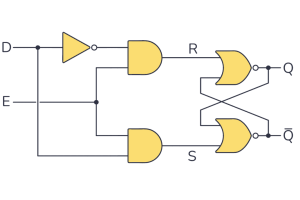
Förstå D -spärrarna i digitala system
på 2024/08/12
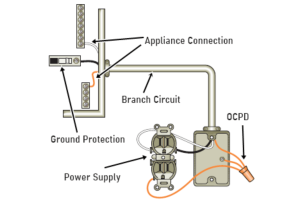
Hur fungerar överströmsskyddsanordningar?
på 2024/08/12
Populära inlägg
-
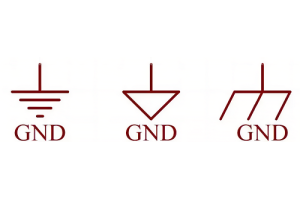
Vad är GND i kretsen?
på 1970/01/1 3117
-

RJ-45 Connector Guide: RJ-45 Connector Color Codes, Wiring Schemes, R-J45 Applications, RJ-45 Datablad
på 1970/01/1 2679
-
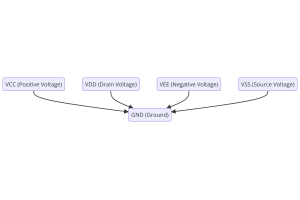
Förstå strömförsörjningsspänningar i elektronik VCC, VDD, VEE, VSS och GND
på 0400/11/15 2222
-

Fiberanslutningstyper: SC vs LC och LC vs MTP
på 1970/01/1 2185
-

Jämförelse mellan DB9 och Rs232
på 1970/01/1 1804
-

Vad är ett LR44 -batteri?
Elektricitet, den allestädes närvarande kraften, genomsyrar tyst alla aspekter av vårt dagliga liv, från triviala prylar till livshotande medicinsk utrustning, det spelar en tyst roll.Men verkligen att ta tag i denna energi, särskilt hur man lagrar och effektivt matar ut den, är ingen enkel uppgift.Det är mot denna bakgrund som den här artikeln kommer att fokusera på en typ av myntcellbat...på 1970/01/1 1778
-

Förstå grunderna: induktansmotstånd och kapacitans
I den intrikata dansen för elektroteknik tar en trio av grundläggande element centrum: induktans, motstånd och kapacitans.Var och en bär unika drag som dikterar de dynamiska rytmerna i elektroniska kretsar.Här går vi in på en resa för att dechiffrera komplexiteten i dessa komponenter, för att avslöja deras distinkta roller och praktiska användningar inom den enorma elektriska orkest...på 1970/01/1 1730
-

CR2430 Batteri Comprehensive Guide: Specifikationer, applikationer och jämförelse med CR2032 -batterier
Vad är CR2430 -batteri?Fördelarna med CR2430 -batterierNormCR2430 BatterilapplikationerCR2430 -motsvarighetCR2430 vs CR2032Batteri CR2430 -storlekVad man ska leta efter när du köper CR2430 och motsvarandeDatablad pdfVanliga frågor Batterier är hjärtat i små elektroniska enheter.Bland de många tillgängliga typerna spelar myntceller en avgörande roll, som vanligtvis finns i kalkylatorer, ...på 1970/01/1 1681
-
Vad är RF och varför använder vi det?
Radiofrekvens (RF) -teknologi är en viktig del av modern trådlös kommunikation, vilket möjliggör dataöverföring över långa avstånd utan fysiska anslutningar.Den här artikeln går in i grunderna i RF och förklarar hur elektromagnetisk strålning (EMR) gör RF -kommunikation möjlig.Vi kommer att utforska principerna för EMR, skapandet och kontrollen av RF-signaler och deras omfattande ...på 1970/01/1 1672
-

Omfattande guide till HFE i transistorer
Transistorer är avgörande komponenter i moderna elektroniska enheter, vilket möjliggör signalförstärkning och kontroll.Den här artikeln går in i kunskapen kring HFE, inklusive hur man väljer en transistors HFE -värde, hur man hittar HFE och förstärkningen av olika typer av transistorer.Genom vår utforskning av HFE får vi en djupare förståelse för hur transistorer fungerar och dera...på 5600/11/15 1640














































